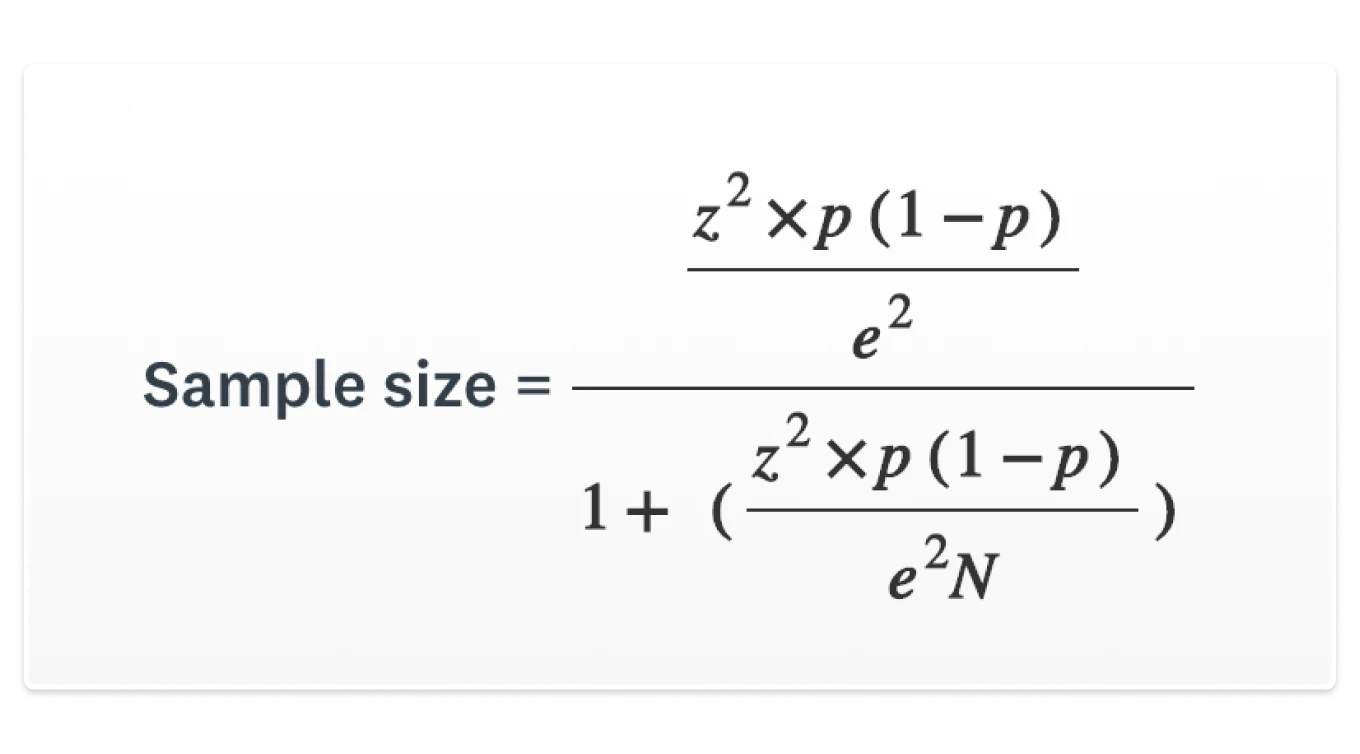How to Define a Proper Sample Size for Your Study|2025

Learn how to define a proper sample size for your study. Explore key factors and techniques to ensure accurate, reliable, and meaningful research results.

In research, selecting an appropriate sample size is crucial to ensure that the results of the study are both valid and reliable. A sample that is too small may fail to detect significant effects, while a sample that is too large can waste resources and time. This paper explores how to define a proper sample size for your study, providing insights into various methods for calculating sample sizes, understanding the concept in both qualitative and quantitative research, and offering real-world examples.

Table of Contents

Understanding Sample Size

Sample size refers to the number of observations or participants included in a study. In statistical analysis, the sample size is critical because it influences the study’s ability to detect differences or relationships, its generalizability to a broader population, and the power of the tests used. The goal of determining the right sample size is to achieve a balance between the precision of the results and the resources required to conduct the study.

Why Sample Size Matters

Statistical Power: A larger sample size increases the likelihood of detecting a statistically significant effect when one exists. Statistical power refers to the probability that a test will correctly reject the null hypothesis (i.e., find a real effect when it exists).
Precision of Estimates: A larger sample provides more reliable estimates of the population parameters, such as the mean or proportion, leading to narrower confidence intervals.
Cost-Effectiveness: On the other hand, too large a sample size can be a waste of resources, time, and effort. It is important to calculate the smallest sample size needed to meet the objectives without unnecessary expenditure.

How to Calculate Sample Size in Research

The process of calculating sample size depends on several factors, including the desired confidence level, margin of error, and variability in the population. In most cases, researchers use the following formula to calculate sample size for estimating a population mean or proportion:

Sample Size Formula for a Proportion:

$\frac{{Z^2 \cdot p(1-p)}}{{E^2}}$

Where:

n = Sample size
Z = Z-score, corresponding to the confidence level (e.g., 1.96 for 95% confidence)
p = Estimated proportion of the population (if unknown, use 0.5 as the conservative estimate)
E = Desired margin of error (e.g., ±5%)

For a population mean, the formula is:

$\frac{{Z^2 \cdot \sigma^2}}{{E^2}}$

Where:

σ = Standard deviation of the population
E = Desired margin of error
Z = Z-score for the desired confidence level

Key Factors in Determining Sample Size

Confidence Level: The confidence level is the probability that the sample accurately reflects the population within the margin of error. A 95% confidence level is commonly used in research, though other levels (e.g., 90%, 99%) can also be applied depending on the study’s requirements.
Margin of Error: The margin of error, often expressed as a percentage, indicates how much the sample results might differ from the true population value. A smaller margin of error requires a larger sample size.
Population Variability: The variability, or standard deviation, of the population impacts the sample size. If the population is highly variable, a larger sample is required to obtain accurate estimates.
Power of the Study: Power analysis is used to determine the sample size needed to detect an effect of a given size. A common power level is 80%, meaning the test has an 80% chance of detecting a true effect if it exists.
Population Size: If the total population is small, the sample size might need to be adjusted using a finite population correction.

How to Define a Proper Sample Size for Your Study Example

Let’s consider an example to demonstrate how to define a proper sample size for your study. Suppose you are conducting a study on the effectiveness of a new drug for reducing blood pressure in adults. You want to estimate the mean reduction in blood pressure with a 95% confidence level and a margin of error of ±2 mmHg.

Assume the standard deviation of blood pressure reductions in the population is estimated to be 10 mmHg. Using the sample size formula for a population mean:

$\frac{{(1.96)^2 \cdot (10)^2}}{{(2)^2}} = \frac{{3.8416 \cdot 100}}{{4}} = 96.04$

Thus, a sample size of 97 participants would be needed to achieve the desired precision.

How to Determine Sample Size in Research Methodology

In quantitative research, determining the sample size involves several steps:

Identify Study Objectives: Clarify the study’s purpose—whether it’s estimating a population parameter, testing a hypothesis, or evaluating the effectiveness of an intervention.
Select the Type of Analysis: Decide on the statistical tests you will use. For example, if you’re comparing means, you might use a t-test or ANOVA, which will impact the sample size calculation.
Set Parameters: Determine the desired confidence level, margin of error, and the expected effect size or variability. These parameters are critical in calculating the minimum sample size.
Conduct Power Analysis: Power analysis helps you determine the sample size required to detect a given effect size with a specific probability (usually 80% or 90%). Tools such as G*Power can be used for power analysis.
Adjust for Practical Considerations: Factor in issues like dropout rates or nonresponse in surveys. These adjustments ensure that the final sample size is sufficient even if some participants are lost during the study.

What is a Good Sample Size for a Study?

A “good” sample size for a study depends on the specific objectives, the type of research, and the resources available. A study with too small a sample size risks Type II errors (failing to detect a real effect), while too large a sample size can lead to unnecessary costs and logistical challenges.

Generally, a sample size of 30 or more is considered the minimum for many statistical analyses, though smaller sample sizes can be acceptable in exploratory studies or studies with very homogeneous populations. For more precise estimates, or when dealing with small populations, larger sample sizes are often necessary.

How to Determine Sample Size for Known Population

When the population size is known and finite, sample size calculations must account for the size of the population. The finite population correction (FPC) is used to adjust the sample size formula when the population size is not infinitely large. The corrected sample size formula is:

$nadj=n1+n−1Nn_{adj} = \frac{{n}}{{1 + \frac{{n-1}}{{N}}}}$

Where:

n = Sample size calculated without correction
N = Population size
n_{adj} = Adjusted sample size for a finite population

This adjustment is particularly relevant when dealing with small populations, ensuring that the sample size is not unnecessarily large.

Sample Size in Research Example

For instance, consider a study examining the relationship between exercise and heart health in a small town with a population of 1,000 adults. After calculating an initial sample size of 278 using the standard formula, applying the finite population correction might reduce the required sample size to around 278 adjusted for the town’s total population.

Sample Size Formula

As discussed earlier, the formula for calculating sample size varies depending on whether you’re estimating a population mean or a proportion. In practice, many researchers use online calculators or statistical software (e.g., SPSS, R, or SAS) to simplify these calculations. These tools allow researchers to input parameters such as confidence level, margin of error, and population variability, which then calculate the required sample size.

How to Define a Proper Sample Size for Your Study in Quantitative Research

In quantitative research, defining a proper sample size is often more complex than in qualitative studies due to the reliance on statistical tests to analyze numerical data. Quantitative studies typically involve hypotheses testing, regression analysis, correlation studies, or analysis of variance (ANOVA), all of which require careful calculation of the sample size.

In this context, the following methods are used:

Hypothesis Testing: Sample size calculations for hypothesis testing typically rely on the effect size, alpha level (significance level), and desired power. A commonly used formula for hypothesis testing is: $\frac{{(Z_{\alpha/2} + Z_{\beta})^2 \cdot (\sigma^2)}}{{\delta^2}}$ Where:
- Z_{\alpha/2} = Z-value for the desired significance level
- Z_{\beta} = Z-value for the desired power
- σ = Standard deviation
- δ = Minimum detectable effect (effect size)
Regression Analysis: In regression studies, the sample size is calculated based on the number of predictors and the desired power. A larger sample size is required for more predictors to maintain the power of the test.
Pilot Studies: For exploratory quantitative research, pilot studies are often conducted to estimate the sample size. The data from the pilot study can provide estimates of the standard deviation, which can then be used to refine the sample size calculations.

Conclusion

Defining a proper sample size is an essential aspect of research design. By understanding the key factors—such as confidence level, margin of error, population variability, and power—you can calculate a sample size that ensures your study’s results are valid, reliable, and cost-effective. Whether you are conducting a simple descriptive study or a complex regression analysis, calculating the correct sample size is vital for the success of your research. Always ensure that the sample size is neither too small to miss meaningful results nor too large to waste valuable resources.

By using the appropriate sample size formulas and statistical tools, researchers can confidently design studies that yield accurate and generalizable findings.